Dấu giá trị tuyệt đối là một kiến thức rất quen thuộc trong Toán học và cách giải bất phương trình chứa dấu giá trị tuyệt đối cũng là một phần quan trọng không kém của chương trình học. Vậy thế nào là bất phương trình có chứa dấu giá trị tuyệt đối và cách giải đối với loại phương trình này là gì?
Lý thuyết tổng quan về phương trình chứa dấu giá trị tuyệt đối
Lý thuyết về giá trị tuyệt đối
Giá trị tuyệt đối còn được biết đến là môđun của số thực a. Giá trị tuyệt đối của số a được ký hiệu là |a| và trong toán học, giá trị tuyệt đối của a sẽ được định nghĩa như sau:
- |a| = a khi a ≥ 0
- |a| = -a khi a < 0
Giá trị tuyệt đối của số 0 được ký hiệu là |0| và |0| = 0. Hiểu theo cách đơn giản, giá trị tuyệt đối của một số nghĩa là khoảng cách từ số đó đến 0. Do đó, giá trị tuyệt đối của số dương là chính bản thân số đó, giá trị tuyệt đối của số âm chính là số đối của số đó.
Tính chất của giá trị tuyệt đối
Tiếp theo, hãy cùng tìm hiểu đến những tính chất cần biết của dấu giá trị tuyệt đối nhé.
- Giá trị tuyệt đối tại tất cả mọi số đều sẽ không âm.
- Hai số có giá trị bằng nhau hoặc 2 số đối với nhau trên trục số sẽ có giá trị tuyệt đối bằng nhau. Tương tự, hai số có giá trị tuyệt đối bằng nhau thì sẽ là 2 số bằng nhau hoặc là 2 số đối nhau trên trục số.
- Mọi số đều sẽ có giá trị lớn hơn hoặc bằng với số đối của giá trị tuyệt đối của bản thân số đó, đồng thời sẽ nhỏ hơn hoặc bằng với giá trị tuyệt đối của số đó.
- Trong 2 số âm, số nào có giá trị tuyệt đối nhỏ hơn sẽ là số lớn hơn. Ngược lại, trong 2 số dương, số nào có giá trị tuyệt đối nhỏ hơn sẽ là số nhỏ hơn.
- Giá trị tuyệt đối của thương sẽ là thương của 2 giá trị tuyệt đối. Tương tự, giá trị tuyệt đối của một tích sẽ bằng tích của 2 giá trị tuyệt đối.
- Bình phương của một giá trị tuyệt đối bằng với bình phương của chính số đó.
- Tổng của 2 giá trị tuyệt đối sẽ luôn luôn lớn hơn hoặc bằng với giá trị tuyệt đối của tổng 2 số đó.
Dấu giá trị tuyệt đối được ứng dụng rất nhiều trong lĩnh vực Toán học, bao gồm đối với các hàm toán, những số phức, trường và vecto,… giải phương trình chứa dấu giá trị tuyệt đối là kiến thức nền tảng mà bất cứ học sinh nào cũng cần phải biết.
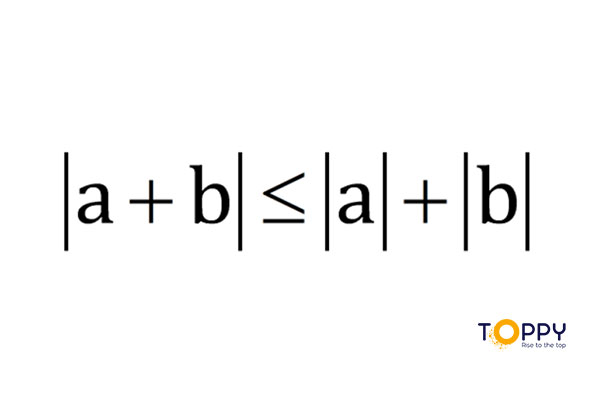
Những tính chất của giá trị tuyệt đối
Thế nào là phương trình và bất phương trình chứa dấu giá trị tuyệt đối?
Phương trình chứa dấu giá trị tuyệt đối là phương trình được viết dưới dạng |f(x)| = |g(x)| hoặc |f(x)| = g(x). Bất phương trình chứa dấu giá trị tuyệt đối có 2 dạng cơ bản là |f(x)| > |g(x)| và |f(x)| > g(x).
Phương trình chứa dấu giá trị tuyệt đối lớp 8 là những kiến thức cơ bản nhất về dấu giá trị tuyệt đối dành cho học sinh. Nắm được cách giải phương trình chứa dấu giá trị tuyệt đối, cách giải BPT mang dấu giá trị tuyệt đối sẽ giúp cho bạn giải quyết được nhiều vấn đề liên quan ở các bài toán phức tạp hơn.
Quy trình và cách giải bất phương trình chứa dấu giá trị tuyệt đối
Quy trình giải BPT chứa dấu giá trị tuyệt đối
- Bước 1: Sau khi phân tích đề bài, các bạn cần phải áp dụng những định nghĩa về dấu giá trị tuyệt đối để loại bỏ đi dấu giá trị tuyệt đối trong bài toán.
- Bước 2: Giải bất phương trình đã được loại bỏ đi dấu giá trị tuyệt đối.
- Bước 3: Sau khi giải ra được nhiều trường hợp, chúng ta sẽ kết hợp với điều kiện để chọn nghiệm thích hợp nhất dành cho phương trình đang được xét.
- Bước 4: Kết luận đáp án của bài toán.

Quy trình giải bất phương trình chứa dấu giá trị tuyệt đối
Để khử dấu giá trị tuyệt đối, các bạn có thể sử dụng 3 cách sau đây:
- Sử dụng định nghĩa của dấu giá trị tuyệt đối, tính chất của dấu giá trị tuyệt đối.
- Bình phương 2 vế trong bất phương trình chứa dấu giá trị tuyệt đối.
- Đặt ẩn phụ để giải bất phương trình.
Cách giải bất phương trình chứa dấu giá trị tuyệt đối
Để giải BPT có dấu giá trị tuyệt đối, trước tiên cần phải xác định các dạng cơ bản, bao gồm:
- Dạng 1: |f(x)| > |g(x)|
- Dạng 2: |f(x)| > g(x)
- Dạng 3: |f(x)| < g(x)
Khi giải dạng bất phương trình này, chúng ta sử dụng 3 phương pháp chính, bao gồm khử căn bằng định nghĩa, phương pháp lập bảng và phương pháp biến đổi tương đương.

Các phương pháp giải bất phương trình
Phương pháp khử căn bằng định nghĩa
- |f(x)| = f(x) khi f(x) > 0.
- |f(x)| = -f(x) khi f(x) < 0.
Phương pháp lập bảng
Để khử giá trị tuyệt đối khi giải BPT có chứa dấu giá trị tuyệt đối bằng cách lập bảng, chúng ta cần phải kết hợp bảng xét dấu nhị thức bậc nhất cùng tam thức bậc hai.
Phương pháp biến đổi tương đương
- Bất phương trình |f(x)| > |g(x)| (f(x))2 > (g(x))2.
- Bất phương trình |f(x)| > |g(x)| g(x) < 0 hoặc [g(x) 0 và f2(x) > g2(x)].
- Bất phương trình |f(x)| > |g(x)| g(x) >0 và f(x)2 < [g(x)]2.